目录：

本文是我学习《数字信号处理 – 基于计算机的方法》第四版的笔记

信号与信号处理

信号

信号分类

振幅
时间
- 连续时间信号
  - 振幅也连续：模拟信号
- 离散时间信号
  - 振幅离散：数字信号

复数信号和解析信号

复数信号

Why?
- 信号表示更加复杂（相位，幅度） -> 信息量很大 -> 信号处理更加简单，易于处理
希尔伯特变换 HT
- $h_{HT} = \frac{1}{\pi t}$
- $H_{HT}(j\Omega) = \begin{cases} -j & \Omega > 0 \\ j & \Omega < 0 \end{cases} $

实数信号

实数信号
- FT性质 => 幅度偶对称，相位奇对称
- 正频率 + 负频率 $X(j\Omega) = X_p(j\Omega)+X_n(j\Omega)$
- 经过HT => $\hat{X}(j\Omega) = -j X_p(j\Omega)+jX_n(j\Omega)$ => $\hat{x}(t)$也是实数信号

解析信号

=> 解析信号 $y(t) = x(t) + j\hat{x}(t)$

$x(t), \hat{x}(t)$ 为同相分量和正交分量

$Y(j\Omega) = X(j\Omega)+j\hat{X}(j\Omega) = 2 X_p(j\Omega)$

我们可以看出解析信号只包含正频率的部分

信号运算

简单运算
- 衰减
- 延迟 $y(t) = x(t-t_0)$
- 相加，相乘
- 积分 $y(t) = \int_{-\infty}^{t}x(\tau) d\tau$
- 微分 $y(t) = \frac{dx(t)}{dt}$
- 傅里叶变换Fourier Transform(FT) $X(j\Omega) = \int_{-\infty}^{+\infty}x(t) e^{-j\Omega t} dt$
滤波
- $y(t) = \int_{-\infty}^{+\infty} h(t-\tau)x(\tau)d\tau$
- 低通，高通，带通
- 带阻（陷波器3）
- 多频带滤波器：多个通带阻带
- 梳状滤波器：阻断某个低频的整数倍

调制

Why?
- 低频信号无法直接用于传输
- 调制到高频进行传输- 原理：利用信号的振幅、相位、频率表示信号

时域离散时间信号

离散时间信号， Why？

现代计算机、微处理器、嵌入式设备都是处理数字信号的，但是我们的物理世界充斥着连续信号（模拟信号），如声音信号等。而直接处理模拟信号是比较困难的（1G通信），设备器件做的很大（大哥大），而且不便于加密（你树根天线就能窃听到隔壁老王在电话里说什么）。这就涉及到模拟信号数字化（采样，或者抽样），转换为数字信号进行处理。

时域表示

采样： $x[n] = x_a{(t)}|_{t = nT} = x_a(nT)$

采样频率（抽样频率）： $F_t = \frac{1}{T}$

采样得到的值由于ADC（数模转换器）的精度问题（例如12 Bit ADC）有舍入的问题。

频域表示

归一化角频率：$\omega_c$ 为归一化角频率，因为样本$n$是无量纲的，所以应该是弧度/样本，且

$$
\omega = 2\pi f
$$

$f$ 是归一化角频率，单位是周期/样本，即一个样本多少周期

运算

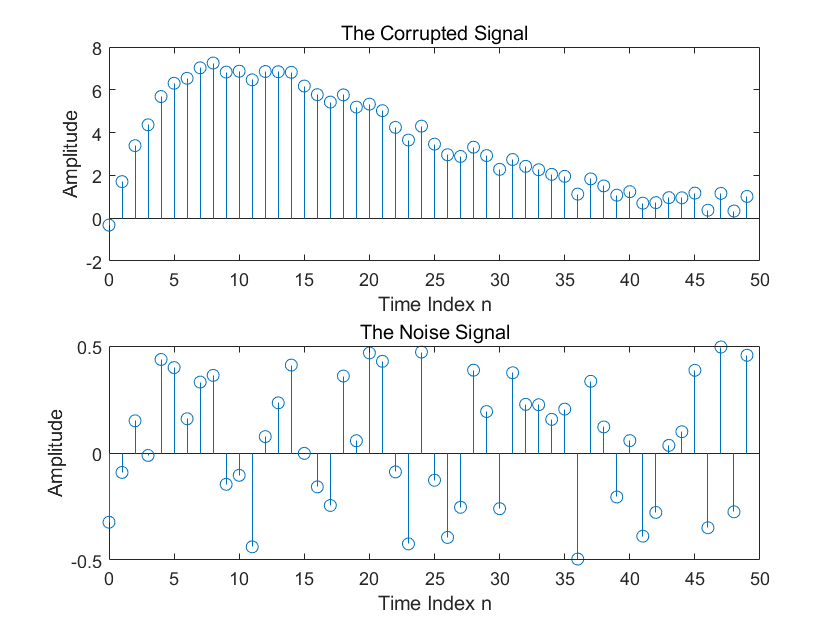
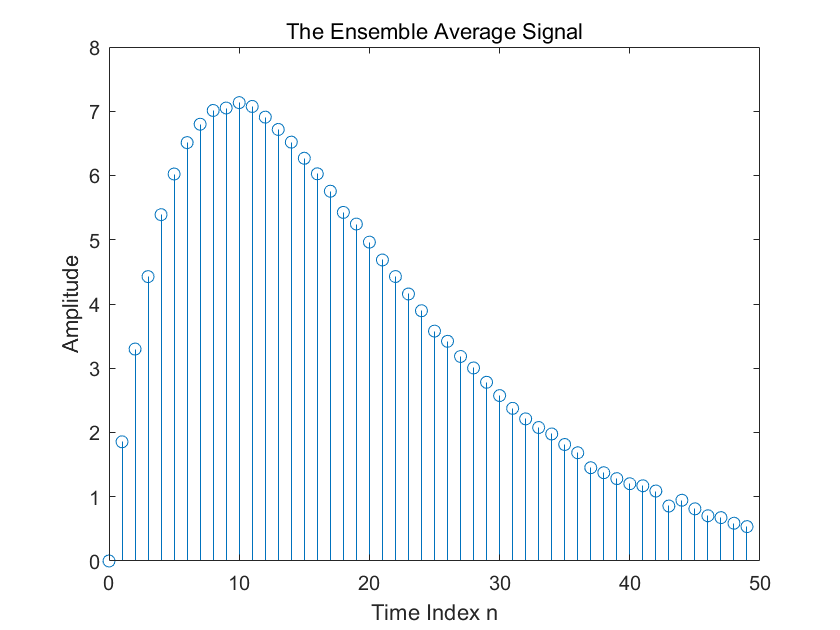
例子2.1：集合平均

$s[n]=2[n(0.9)^n]$ 和噪声$d(n)$，受干扰后的集合平均可以减少干扰影响

% Program_2_1
% Generation of the ensemble average
N = 50; % total number
n = 0 : N-1;
s = 2*(n.*0.9.^n); % generate the original signal s[n]
rng();
d = rand(N, 1) - 0.5; % generate the noise signal d[n]

x1 = s+d'; % the corrupted signal

% Plot the corrupted signal
subplot(2,1,1)
stem(n, x1);
xlabel('Time Index n')
ylabel('Amplitude')
title('The Corrupted Signal')

% Plot the Noise Signal
subplot(2,1,2)
stem(n, d)
xlabel('Time Index n')
ylabel('Amplitude')
title('The Noise Signal')

% Ensemble average
for m = 1:50
    rng();
    noise = rand(N,1) - 0.5;
    x = s + noise';
    x1 = x1 + x;
end
x1 = x1 / N;

% Plot the ensemble average signal
figure;
stem(n, x1);
xlabel('Time Index n')
ylabel('Amplitude')
title('The Ensemble Average Signal')

卷积

使用函数 conv即可作为卷积运算

抽样率转换

抽样率转换比: $\frac{F_T^{‘}}{F_T} = R$, $F_T$ 是原本的抽样率, 再拿$F_T^{‘}$ 去抽样

序列分类

周期、非周期
能量信号、功率信号

木慕的博客

数字信号处理 -- 基于计算机方法